Mastering algebra is a fundamental component of a student’s mathematical journey, and it often presents various challenges, including some of the hardest algebra problems. These problems can range from complex equations to intricate formulas, requiring students to apply critical thinking and problem-solving skills. Understanding algebraic equations, formulas, and solutions is essential for tackling these hardest algebra problems, as they serve as the building blocks for more advanced mathematical concepts.
Encountering the hardest algebra problems can be a daunting yet rewarding experience for students. These challenging problems demand a deep understanding of algebraic principles and the ability to navigate through intricate equations and formulas. By mastering these difficult algebra problems, students not only strengthen their problem-solving skills but also gain confidence in their mathematical abilities. Therefore, grasping the intricacies of algebraic equations and formulas is crucial for students to conquer the hardest algebra problems and excel in their mathematical journey.
1. The Infamous Quadratic Equation
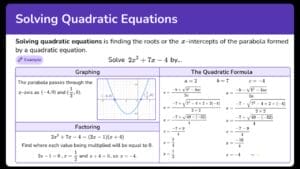
Quadratic equations are one of the hardest algebra problems that students encounter, yet they are fundamental in understanding the behavior of various mathematical functions. These equations are of particular significance in algebra due to their ability to model a wide range of real-world phenomena, such as projectile motion and the shape of parabolic curves. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. To solve such equations, one can use the quadratic formula, which states that the solutions for x can be found using the formula x = (-b ± √(b^2 – 4ac)) / (2a). This formula provides a systematic method for finding the roots of a quadratic equation, even in cases where the solutions are complex numbers.
To illustrate the process of solving one of the hardest algebra problems, consider the complex quadratic equation 3x^2 + 2x + 5 = 0.
By applying the quadratic formula, we can determine the solutions for x.
Plugging the values of a = 3, b = 2, and c = 5 into the formula, we obtain x = (-2 ± √(2^2 – 4*3*5)) / (2*3).
Simplifying further, we find x = (-2 ± √(-56)) / 6. Since the discriminant (√(-56)) is an imaginary number, the solutions for x will also be complex.
Thus, the quadratic equation has two complex roots: x = (-2 + √(-56)) / 6 and x = (-2 – √(-56)) / 6. This demonstrates the intricate nature of solving the hardest algebra problems involving complex quadratic equations.
2. Conquering Systems of Linear Equations
Systems of linear equations are fundamental to the study of algebra and have wide-ranging applications in real-world problem-solving. In essence, a system of linear equations involves a set of two or more linear equations to find a common solution that satisfies all the equations simultaneously. This concept is crucial in modeling various real-life scenarios, such as determining the optimal combination of resources in production, analyzing the intersection points of lines, and formulating strategies in game theory. One of the hardest algebra problems often involves solving complex systems of linear equations, which requires a deep understanding of the underlying principles and the ability to apply different solution methods effectively.
Solving systems of linear equations can be approached through various methods, including substitution, elimination, or matrix techniques. Substitution involves isolating a variable in one equation and then substituting that expression into the other equation, ultimately leading to the solution for the variables. On the other hand, elimination involves manipulating the equations to eliminate one variable by adding or subtracting the equations, eventually leading to a single equation with one variable. Matrix methods, such as Gaussian elimination or matrix inversion, provide a systematic approach to solving systems of linear equations by representing the equations in matrix form and applying operations to simplify and solve for the variables. Tackling the hardest algebra problems often requires proficiency in all these methods and the ability to select the most suitable approach for a given system of equations, demonstrating a high level of problem-solving skills and mathematical acumen.

3. Unraveling the Mysteries of Polynomial Factoring
Polynomial factoring is a crucial concept in algebra that significantly simplifies complex algebraic expressions, which are often considered some of the hardest algebra problems. By factoring polynomials, we can break down complicated expressions into simpler forms, making it easier to analyze and manipulate them. This process is particularly relevant in solving equations, graphing functions, and understanding the behavior of mathematical models. Different techniques can be employed for factoring polynomials, including the difference of squares, grouping, and the quadratic formula. Each method has its own set of rules and strategies, allowing mathematicians to approach various types of polynomials with different structures and complexities. Understanding these techniques is essential for tackling some of the hardest algebra problems and mastering the art of polynomial factoring.
To showcase the intricacy of polynomial factoring, let’s delve into a complex polynomial expression often considered one of the hardest algebra problems. By applying different factoring techniques, we can guide readers by breaking down the expression into its simplest form. This exercise demonstrates the application of factoring methods and highlights the importance of patience, precision, and problem-solving skills in addressing the hardest algebra problems. Through this example, readers can better understand the power of polynomial factoring and its role in unraveling the mysteries of complex algebraic expressions.
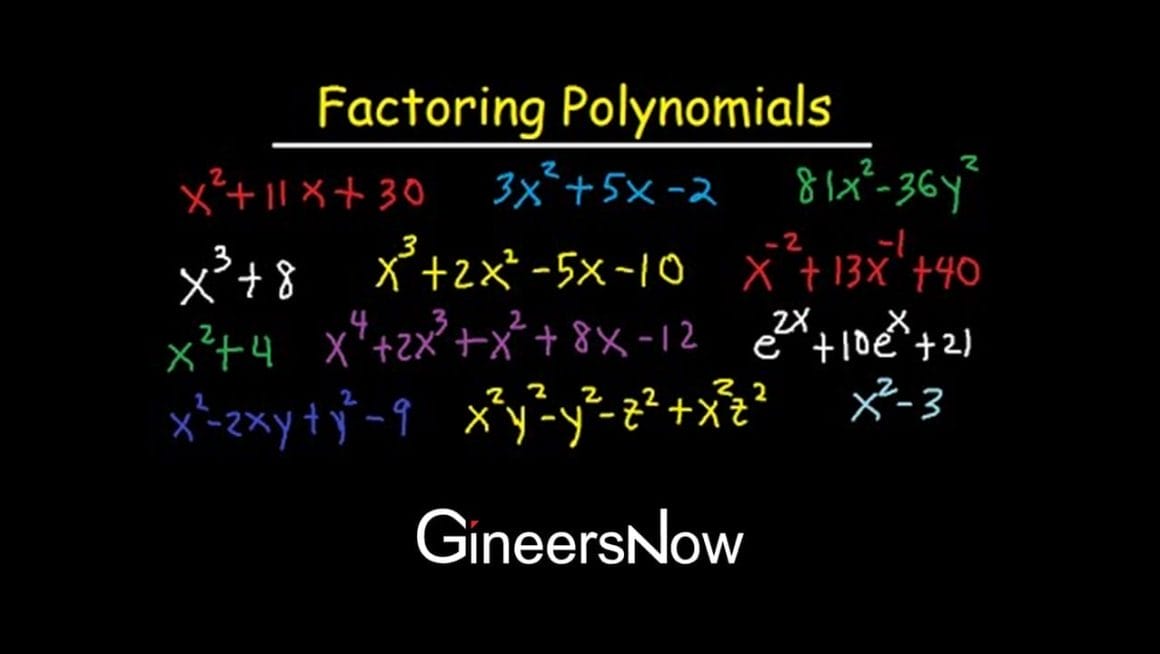
Concluding Thoughts: 3 of the World’s Hardest Algebra Problems
Mastering the hardest algebra problems is essential for building a robust foundation in algebra. By tackling challenging algebraic equations, individuals can enhance their understanding of key concepts, such as equations, formulas, and solutions. Solving difficult algebra problems sharpens problem-solving skills and fosters a deeper comprehension of algebraic principles. Therefore, by embracing the hardest algebra problems, readers can pave the way for a more comprehensive mastery of algebra and set themselves up for success in more advanced mathematical pursuits.












