Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is an essential part of mathematics, frequently used in various fields such as physics, engineering, and astronomy. In this blog post, we will explore three of the most hardest trigonometry problems that have puzzled mathematicians and students alike.
1. Problem 1: Trigonometric Ratios Puzzle
Trigonometry problems can be challenging, especially when they involve finding the values of trigonometric ratios for specific angles within a given triangle. This requires a deep understanding of sine, cosine, and tangent functions and their applications in solving real-world problems. When tackling such trigonometry problems, it’s important to approach them methodically and systematically. We will discuss the approach to solving these difficult trigonometry problems and provide step-by-step guidance to help you navigate through the complexities of trigonometric ratios and their applications within triangles. By breaking down the problem and understanding the fundamentals of trigonometry, you can confidently tackle these challenging trigonometry problems with precision and accuracy.
Example:
Consider a trigonometry problem where you are given a right-angled triangle with an angle of 30 degrees. The task is to find the values of sine, cosine, and tangent for this angle within the triangle. To solve this problem, you would first identify the sides of the triangle relative to the given angle and then apply the sine, cosine, and tangent functions accordingly. By understanding the fundamental principles of trigonometry, you can systematically approach the problem, calculate the trigonometric ratios, and apply them to real-world scenarios, such as determining distances, heights, or angles in various contexts. This example demonstrates the application of trigonometric concepts to solve practical problems and highlights the importance of a structured approach when dealing with challenging trigonometry problems.

2. Problem 2: Trigonometric Functions Conundrum
Trigonometry problems often delve into the intricate relationships between trigonometric functions, such as sine, cosine, and tangent, and their properties. This challenges the problem-solver to manipulate and simplify trigonometric expressions to arrive at a specific solution. Tackling complex trigonometry problems involves breaking down the problem and offering insights into the intricate nature of these functions, requiring a deep understanding of their properties and how they interact with each other. Students may find these problems challenging, but with the right approach and a solid grasp of trigonometric principles, they can successfully navigate the conundrum of trigonometry problems.
Example:
For example, a trigonometry problem may ask students to simplify an expression involving multiple trigonometric functions, such as sin(x) + cos(x) / tan(x). To solve this, students must apply the fundamental identities of trigonometric functions and manipulate the expression to simplify it into a more manageable form. This process often entails recognizing patterns and relationships between trigonometric functions, ultimately leading to a specific solution. By understanding the properties and behaviors of trigonometric functions, students can effectively tackle such complex problems and arrive at the correct answers.
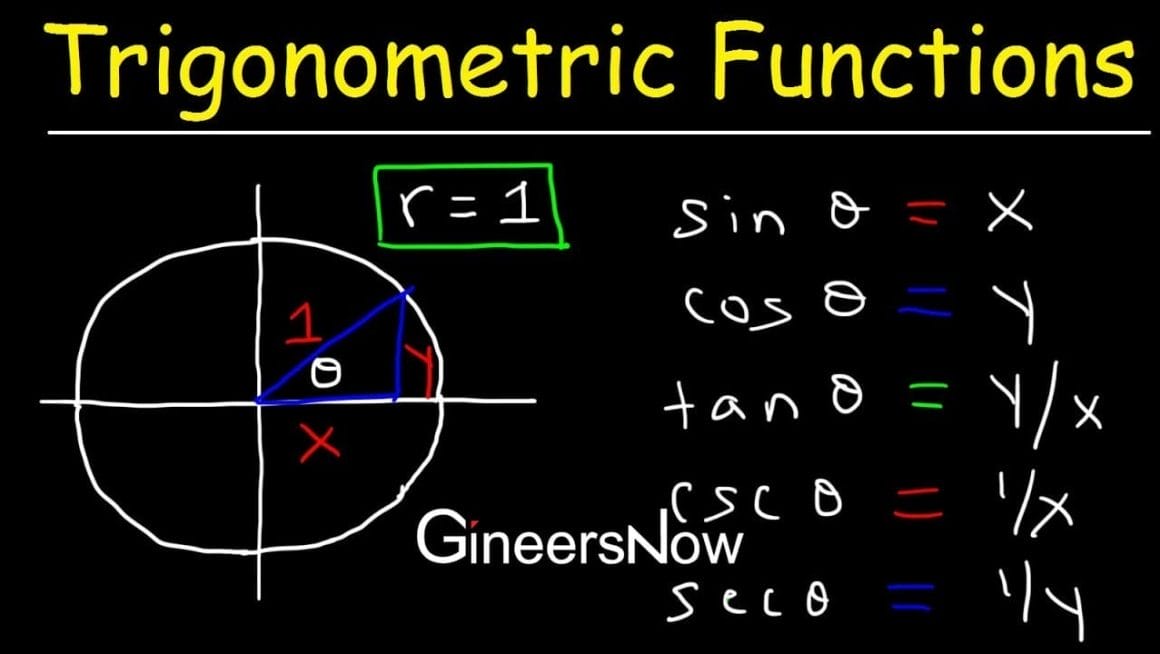
3. Problem 3: Trigonometric Solutions Enigma
Trigonometry problems can present challenging scenarios where multiple trigonometric equations must be solved simultaneously to find a triangle’s unknown angles and sides. These problems require a combination of algebraic manipulation and trigonometric identities to arrive at the correct solutions. To tackle the hardest trigonometry problems, it is essential to employ strategies for approaching and solving them effectively. By understanding the application of trigonometric identities and utilizing algebraic manipulation, one can successfully navigate through the complexities of these trigonometry problems and arrive at accurate solutions.
Example:
Trigonometry problems can present challenging scenarios where multiple trigonometric equations must be solved simultaneously to find a triangle’s unknown angles and sides. For example, consider a scenario where a triangle has two sides of lengths 5 and 7, and the angle between them is unknown. To find the value of the unknown angle, one needs to employ trigonometric identities and algebraic manipulation to solve for the angle using the given side lengths and the properties of trigonometric functions. By understanding the application of trigonometric identities and utilizing algebraic manipulation, one can successfully navigate through the complexities of these trigonometry problems and arrive at accurate solutions.

Conclusion: Hardest Trigonometry Problems
Trigonometry problems can be notoriously tricky, but these challenges can be overcome with a clear understanding of trigonometric functions and ratios, as well as a systematic approach to problem-solving. By unraveling the complexities of these three demanding problems, we hope to enhance your grasp of trigonometry and inspire confidence in tackling even the most formidable trigonometric puzzles.












